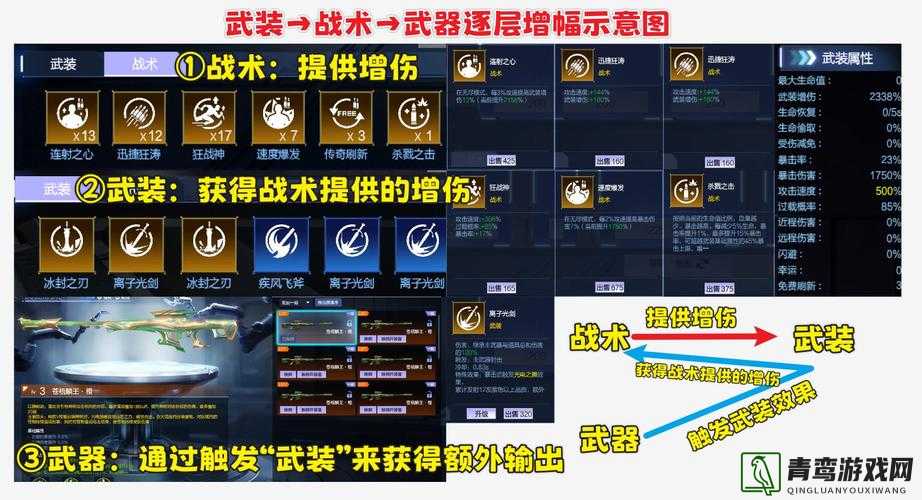
x7x7x7 任意噪：关于它的深入分析与全面解读

在数学的广袤领域中，存在着许多引人深思且具有独特性质的概念和表达式。其中，“$x^7x^7x^7$ 任意噪”这一表达式或许并不为大众所熟知，但它却蕴含着丰富的内涵和值得深入探讨的价值。

让我们来简单分析一下“$x^7x^7x^7$”这个部分。$x$ 的$7$次方表示$x$连乘$7$次，这是一个非常基础且常见的幂运算形式。当$x$取不同的值时，$x^7$的值也会相应地发生变化。它可以是正数、负数或$0$，这使得整个表达式具有了极大的灵活性和多样性。而连续三个$x^7$相乘，进一步增加了其复杂性和可能展现出的特性。

那么，所谓的“任意噪”又意味着什么呢？“噪”在这里可以理解为一种不确定性或随机性的因素。这可能暗示着在对这个表达式进行研究和分析时，存在着各种无法完全预测或确定的情况。它可能与输入的变量$x$的取值范围、取值的随机性，或者在某些特定条件下所表现出的难以捉摸的性质相关。

从数学的角度来看，对“$x^7x^7x^7$ 任意噪”进行深入分析可以涉及多个方面。可以研究它在不同定义域和值域下的取值规律。通过对不同$x$值的代入计算，可以发现一些有趣的模式和趋势，例如是否存在特定的取值范围使得表达式的值呈现出某种周期性、单调性或者其他规律性的变化。

进一步地，可以探讨它在数学运算中的性质。例如，与其他常见的数学运算如加法、减法、乘法、除法等的结合会产生怎样的结果，是否存在一些特殊的运算技巧或规律可以利用来简化计算或得出更有意义的结论。

从函数的角度来看，“$x^7x^7x^7$ 任意噪”可以看作是一个函数表达式。那么，可以研究它的函数图像、单调性、极值点、零点等性质。通过绘制函数图像，可以直观地了解表达式在不同$x$取值范围内的大致形态和变化趋势，从而更好地理解其特性。

在实际应用中，也可能存在与“$x^7x^7x^7$ 任意噪”相关的领域或问题。例如，在科学研究中，某些物理模型、化学反应或者工程计算中，可能会涉及到类似具有不确定性和复杂性的表达式。通过对这种表达式的深入分析和理解，可以为解决实际问题提供理论支持和方法指导。

要全面解读“$x^7x^7x^7$ 任意噪”并非一件容易的事情。由于其中存在着不确定性和随机性的因素，可能需要运用概率论、统计学等相关知识来进行更深入的研究。也需要借助计算机模拟和数值计算等手段来探索其各种可能的情况和性质。

在研究的过程中，还需要保持开放的思维和创新的精神。因为这种具有任意噪性质的表达式往往会带来一些意想不到的结果和发现，可能会拓展我们对数学和相关领域的认知边界。

“$x^7x^7x^7$ 任意噪”是一个具有一定挑战性和研究价值的数学表达式。通过对它的深入分析与全面解读，我们可以更好地理解幂运算的复杂性、不确定性在数学中的表现形式，以及它们在实际应用中的潜在意义。这不仅有助于推动数学学科的发展，也为解决实际问题提供了新的思路和方法。对于这样一个复杂的表达式，未来还需要更多的学者和研究者投入精力进行深入研究，不断挖掘其中的奥秘和价值，使其在数学和其他领域发挥更大的作用。或许在不久的将来，我们会对“$x^7x^7x^7$ 任意噪”有更全面、更深刻的认识和应用。

对“$x^7x^7x^7$ 任意噪”的研究是一个充满探索和发现可能的领域，需要我们持续地努力和思考，以揭示其中隐藏的数学之美和实际应用的潜力。